NATURAL GOLDEN RATIO
CALCULATION
| List of numbers γ - ζ(3) - √2 - √3 - √5 - φ - α - e - π - δ | |
| Binary | 1.1001111000110111011… |
| Decimal | 1.6180339887498948482… |
| Hexadecimal | 1.9E3779B97F4A7C15F39… |
| Continued fraction |  |
| Algebraic form | 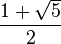 |
Two quantities (positive numbers) a and b are said to be in the golden ratio ϕ if:
This equation unambiguously defines ϕ.
The right equation shows that a = bϕ, which can be substituted in the left part, giving
Cancelling b yields
Multiplying both sides by ϕ and rearranging terms leads to:
The only positive solution to this quadratic equation is
NATURE
- See also: History of aesthetics (pre-20th-century)
Adolf Zeising, whose main interests were mathematics and philosophy, found the golden ratio expressed in the arrangement of branches along the stems of plants and of veins in leaves. He extended his research to the skeletons of animals and the branchings of their veins and nerves, to the proportions of chemical compounds and the geometry of crystals, even to the use of proportion in artistic endeavors. In these phenomena he saw the golden ratio operating as a universal law.[38] Zeising wrote in 1854:
[The Golden Ratio is a universal law] in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form.
—[39]
[edit] Mathematics
[edit] Golden ratio conjugate
The negative root of the quadratic equation for φ (the "conjugate root") is 1 − ϕ ≈ −0.618. The absolute value of this quantity (≈ 0.618) corresponds to the length ratio taken in reverse order (shorter segment length over longer segment length, b / a), and is sometimes referred to as the golden ratio conjugate.[40] It is denoted here by the capital Phi (Φ):
Alternatively, Φ can be expressed as
This illustrates the unique property of the golden ratio among positive numbers, that
or its inverse:
[edit] Short proofs of irrationality
[edit] Contradiction from an expression in lowest terms
Recall that:
- the whole is the longer part plus the shorter part;
- the whole is to the longer part as the longer part is to the shorter part.
If we call the whole n and the longer part m, then the second statement above becomes
- n is to m as m is to n − m,
or, algebraically
To say that φ is rational means that φ is a fraction n/m where n and m are integers. We may take n/m to be in lowest terms and n and m to be positive. But if n/m is in lowest terms, then the identity labeled (*) above says m/(n − m) is in still lower terms. That is a contradiction that follows from the assumption that φ is rational.
[edit] Derivation from irrationality of √5
Another short proof—perhaps more commonly known—of the irrationality of the golden ratio makes use of the closure of rational numbers under addition and multiplication. If 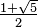 is rational, then
is rational, then  is also rational, which is a contradiction if it is already known that the square root of a non-square natural number is irrational.
is also rational, which is a contradiction if it is already known that the square root of a non-square natural number is irrational.
[edit] Alternate forms
The formula ϕ = 1 + 1/ϕ can be expanded recursively to obtain a continued fraction for the golden ratio:[41]
and its reciprocal:
The convergents of these continued fractions (1, 2, 3/2, 5/3, 8/5, 13/8, … , or 1, 1/2, 2/3, 3/5, 5/8, 8/13, …) are ratios of successive Fibonacci numbers.
The equation ϕ2 = 1 + ϕ likewise produces the continued square root form:
Also:
These correspond to the fact that the length of the diagonal of a regular pentagon is φ times the length of its side, and similar relations in a pentagram.
If x agrees with ϕ to n decimal places, then 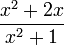 agrees with it to 2n decimal places.
agrees with it to 2n decimal places.
An equation derived in 1994 connects the golden ratio to the Number of the Beast (666):[2]
Which can be combined into the expression:
This relationship depends upon the choice of the degree as the measure of angle, and will not hold when using other units of angular measure.
[edit] Geometry
The number φ turns up frequently in geometry, particularly in figures with pentagonal symmetry. The length of a regular pentagon's diagonal is φ times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles.
There is no known general algorithm to arrange a given number of nodes evenly on a sphere, for any of several definitions of even distribution (see, for example, Thomson problem). However, a useful approximation results from dividing the sphere into parallel bands of equal area and placing one node in each band at longitudes spaced by a golden section of the circle, i.e. 360°/φ ≅ 222.5°. This method was used to arrange the 1500 mirrors of the student-participatory satellite Starshine-3.[42].
[edit] Golden triangle, pentagon and pentagram
[edit] Golden triangle
The golden triangle can be characterised as an isosceles triangle ABC with the property that bisecting the angle C produces a new triangle CXB which is a similar triangle to the original.
If angle BCX = α, then XCA = α because of the bisection, and CAB = α because of the similar triangles; ABC = 2α from the original isosceles symmetry, and BXC = 2α by similarity. The angles in a triangle add up to 180°, so 5α = 180, giving α = 36°. So the angles of the golden triangle are thus 36°-72°-72°. The angles of the remaining obtuse isosceles triangle AXC (sometimes called the golden gnomon) are 36°-36°-108°.
Suppose XB has length 1, and we call BC length φ. Because of the isosceles triangles BC=XC and XC=XA, so these are also length φ. Length AC = AB, therefore equals φ+1. But triangle ABC is similar to triangle CXB, so AC/BC = BC/BX, and so AC also equals φ2. Thus φ2 = φ+1, confirming that φ is indeed the golden ratio.
[edit] Pentagram
- For more details on this topic, see Pentagram.
The golden ratio plays an important role in regular pentagons and pentagrams. Each intersection of edges sections other edges in the golden ratio. Also, the ratio of the length of the shorter segment to the segment bounded by the 2 intersecting edges (a side of the pentagon in the pentagram's center) is φ, as the four-color illustration shows.
The pentagram includes ten isosceles triangles: five acute and five obtuse isosceles triangles. In all of them, the ratio of the longer side to the shorter side is φ. The acute triangles are golden triangles. The obtuse isosceles triangles are golden gnomon.
[edit] Ptolemy's theorem

The golden ratio can also be confirmed by applying Ptolemy's theorem to the quadrilateral formed by removing one vertex from a regular pentagon. If the quadrilateral's long edge and diagonals are b, and short edges are a, then Ptolemy's theorem gives b2 = a2 + ab which yields
[edit] Scalenity of triangles
Consider a triangle with sides of lengths a, b, and c in decreasing order. Define the "scalenity" of the triangle to be the smaller of the two ratios a/b and b/c. The scalenity is always less than φ and can be made as close as desired to φ.[43]
[edit] Relationship to Fibonacci sequence
- For more details on this topic, see Fibonacci number.

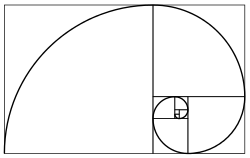
The mathematics of the golden ratio and of the Fibonacci sequence are intimately interconnected. The Fibonacci sequence is:
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
The closed-form expression (known as Binet's formula, even though it was already known by Abraham de Moivre) for the Fibonacci sequence involves the golden ratio:
The golden ratio is the limit of the ratios of successive terms of the Fibonacci sequence (or any Fibonacci-like sequence):
Therefore, if a Fibonacci number is divided by its immediate predecessor in the sequence, the quotient approximates φ; e.g., 987/610 ≈ 1.6180327868852. These approximations are alternately lower and higher than φ, and converge on φ as the Fibonacci numbers increase, and:
Furthermore, the successive powers of φ obey the Fibonacci recurrence:
This identity allows any polynomial in φ to be reduced to a linear expression. For example:
[edit] Other properties
The golden ratio has the simplest expression (and slowest convergence) as a continued fraction expansion of any irrational number (see Alternate forms above). It is, for that reason, one of the worst cases of the Lagrange's approximation theorem. This may be the reason angles close to the golden ratio often show up in phyllotaxis (the growth of plants).
The defining quadratic polynomial and the conjugate relationship lead to decimal values that have their fractional part in common with φ:
The sequence of powers of φ contains these values 0.618…, 1.0, 1.618…, 2.618…; more generally, any power of φ is equal to the sum of the two immediately preceding powers:
As a result, one can easily decompose any power of φ into a multiple of φ and a constant. The multiple and the constant are always adjacent Fibonacci numbers. This leads to another property of the positive powers of φ:
If  , then:
, then:
When the golden ratio is used as the base of a numeral system (see Golden ratio base, sometimes dubbed phinary or φ-nary), every integer has a terminating representation, despite φ being irrational, but every fraction has a non-terminating representation.
The golden ratio is the fundamental unit of the algebraic number field  and is a Pisot-Vijayaraghavan number.
and is a Pisot-Vijayaraghavan number.
Also, 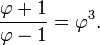
[edit] Decimal expansion
The golden ratio's decimal expansion can be calculated directly from the expression
with √5 ≈ 2.2360679774997896964. The square root of 5 can be calculated with the Babylonian method, starting with an initial estimate such as x₁ = 2 and iterating
for n = 1, 2, 3, …, until the difference between xn and xn−1 becomes zero, to the desired number of digits.
The Babylonian algorithm for √5 is equivalent to Newton's method for solving the equation x2 − 5 = 0. In its more general form, Newton's method can be applied directly to any algebraic equation, including the equation x2 − x − 1 = 0 that defines the golden ratio. This gives an iteration that converges to the golden ratio itself,
for an appropriate initial estimate x₁ such as x₁ = 1. A slightly faster method is to rewrite the equation as x − 1 − 1/x = 0, in which case the Newton iteration becomes
These iterations all converge quadratically; that is, each step roughly doubles the number of correct digits. The golden ratio is therefore relatively easy to compute with arbitrary precision. The time needed to compute n digits of the golden ratio is proportional to the time needed to divide two n-digit numbers. This is considerably faster than known algorithms for the transcendental numbers π and e.
An easily programmed alternative using only integer arithmetic is to calculate two large consecutive Fibonacci numbers and divide them. The ratio of Fibonacci numbers F25001 and F25000, each over 5000 digits, yields over 10,000 significant digits of the golden ratio.
Millions of digits of φ are available (sequence A001622 in OEIS). See the web page of Alexis Irlande for the 17,000,000,000 first digits[44].
[edit] Pyramids
Both Egyptian pyramids and those mathematical regular square pyramids that resemble them can be analyzed with respect to the golden ratio and other ratios.
[edit] Mathematical pyramids and triangles
A pyramid in which the apothem (slant height along the bisector of a face) is equal to φ times the semi-base (half the base width) is sometimes called a golden pyramid. The isosceles triangle that is the face of such a pyramid can be constructed from the two halves of a diagonally split golden rectangle (of size semi-base by apothem), joining the medium-length edges to make the apothem. The height of this pyramid is 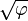 times the semi-base (that is, the slope of the face is
times the semi-base (that is, the slope of the face is 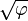 ); the square of the height is equal to the area of a face, φ times the square of the semi-base.
); the square of the height is equal to the area of a face, φ times the square of the semi-base.
The medial right triangle of this "golden" pyramid (see diagram), with sides  is interesting in its own right, demonstrating via the Pythagorean theorem the relationship
is interesting in its own right, demonstrating via the Pythagorean theorem the relationship 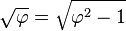 or
or 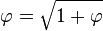 . This "Kepler triangle"[45] is the only right triangle proportion with edge lengths in geometric progression,[46] just as the 3–4–5 triangle is the only right triangle proportion with edge lengths in arithmetic progression. The angle with tangent
. This "Kepler triangle"[45] is the only right triangle proportion with edge lengths in geometric progression,[46] just as the 3–4–5 triangle is the only right triangle proportion with edge lengths in arithmetic progression. The angle with tangent 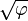 corresponds to the angle that the side of the pyramid makes with respect to the ground, 51.827… degrees (51° 49' 38").[47]
corresponds to the angle that the side of the pyramid makes with respect to the ground, 51.827… degrees (51° 49' 38").[47]
A nearly similar pyramid shape, but with rational proportions, is described in the Rhind Mathematical Papyrus (the source of a large part of modern knowledge of ancient Egyptian mathematics), based on the 3:4:5 triangle;[48] the face slope corresponding to the angle with tangent 4/3 is 53.13 degrees (53 degrees and 8 minutes).[49] The slant height or apothem is 5/3 or 1.666… times the semi-base. The Rhind papyrus has another pyramid problem as well, again with rational slope (expressed as run over rise). Egyptian mathematics did not include the notion of irrational numbers,[50] and the rational inverse slope (run/rise, multiplied by a factor of 7 to convert to their conventional units of palms per cubit) was used in the building of pyramids.[48]
Another mathematical pyramid with proportions almost identical to the "golden" one is the one with perimeter equal to 2π times the height, or h:b = 4:π. This triangle has a face angle of 51.854° (51°51'), very close to the 51.827° of the Kepler triangle. This pyramid relationship corresponds to the coincidental relationship 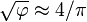 .
.
Egyptian pyramids very close in proportion to these mathematical pyramids are known.[49]
[edit] Egyptian pyramids
In the mid nineteenth century, Röber studied various Egyptian pyramids including Khafre, Menkaure and some of the Gizeh, Sakkara and Abusir groups, and was interpreted as saying that half the base of the side of the pyramid is the middle mean of the side, forming what other authors identified as the Kepl
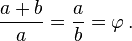
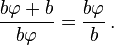

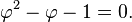

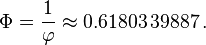
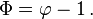
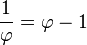

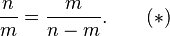
![\varphi = [1; 1, 1, 1, \dots] = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}](http://upload.wikimedia.org/math/8/b/6/8b60ba0565a178cde9cc400bd6c253ab.png)
![\varphi^{-1} = [0; 1, 1, 1, \dots] = 0 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}\,.](http://upload.wikimedia.org/math/c/8/a/c8a67b3ed18d7515b9f54e29358de410.png)
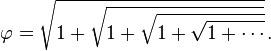
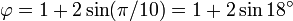
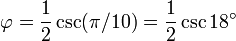
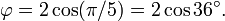




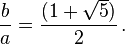
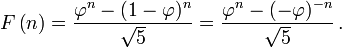
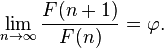
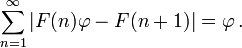

![\begin{align} 3\varphi^3 - 5\varphi^2 + 4 & = 3(\varphi^2 + \varphi) - 5\varphi^2 + 4 \\ & = 3[(\varphi + 1) + \varphi] - 5(\varphi + 1) + 4 \\ & = \varphi + 2 \approx 3.618. \end{align}](http://upload.wikimedia.org/math/0/6/9/06967b74c9f3e771062a76ec3fe7d33e.png)



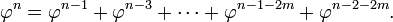

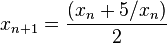



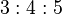 and
and  are of particular interest in relation to Egyptian pyramids.
are of particular interest in relation to Egyptian pyramids.