GOLDEN RATIO
The Golden Ratio
Allah has appointed a measure for all things. (Surat at-Talaq, 3)
… You will not find any flaw in the creation of the All-Merciful. Look again-do you see any gaps? Then look again and again. Your sight will return to you dazzled and exhausted! (Surat al-Mulk, 3-4)
... If a pleasing or exceedingly balanced form is achieved in terms of elements of application or function, then we may look for a function of the Golden Number there ... The Golden Number is a product not of mathematical imagination, but of a natural principle related to the laws of equilibrium. (1)
What do the pyramids in Egypt, Leonardo do Vinci's portrait of the Mona Lisa, sunflowers, the snail, the pine cone and your fingers all have in common?
The answer to this question lies hidden in a sequence of numbers discovered by the Italian mathematician Fibonacci. The characteristic of these numbers, known as the Fibonacci numbers, is that each one consists of the sum of the two numbers before it. (2)
 L. Pisano Fibonacci |
Fibonacci numbers
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …
Fibonacci numbers have an interesting property. When you divide one number in the sequence by the number before it, you obtain numbers very close to one another. In fact, this number is fixed after the 13th in the series. This number is known as the "golden ratio."
233 / 144 = 1.618 377 / 233 = 1.618 610 / 377 = 1.618 987 / 610 = 1.618 1597 / 987 = 1.618 2584 / 1597 = 1.618 |
THE HUMAN BODY AND THE GOLDEN RATIO
When conducting their researches or setting out their products, artists, scientists and designers take the human body, the proportions of which are set out according to the golden ratio, as their measure. Leonardo da Vinci and Le Corbusier took the human body, proportioned according to the golden ratio, as their measure when producing their designs. The human body, proportioned according to the golden ratio, is taken as the basis also in the Neufert, one of the most important reference books of modern-day architects.
 Leonardo da Vinci used the golden ratio in setting out the proportions of the human body. |
THE GOLDEN RATIO IN THE HUMAN BODY
The "ideal" proportional relations that are suggested as existing among various parts of the average human body and that approximately meet the golden ratio values can be set out in a general plan as follows: (3)
The M/m level in the table below is always equivalent to the golden ratio. M/m = 1.618
The first example of the golden ratio in the average human body is that when the distance between the navel and the foot is taken as 1 unit, the height of a human being is equivalent to 1.618. Some other golden proportions in the average human body are:
The distance between the finger tip and the elbow / distance between the wrist and the elbow,
The distance between the shoulder line and the top of the head / head length,
The distance between the navel and the top of the head / the distance between the shoulder line and the top of the head,
The distance between the navel and knee / distance between the knee and the end of the foot.
The Human Hand
Lift your hand from the computer mouse and look at the shape of your index finger. You will in all likelihood witness a golden proportion there.
Our fingers have three sections. The proportion of the first two to the full length of the finger gives the golden ratio (with the exception of the thumbs). You can also see that the proportion of the middle finger to the little finger is also a golden ratio. (4)
You have two hands, and the fingers on them consist of three sections. There are five fingers on each hand, and only eight of these are articulated according to the golden number: 2, 3, 5, and 8 fit the Fibonacci numbers.
The Golden Ratio in the Human Face
There are several golden ratios in the human face. Do not pick up a ruler and try to measure people's faces, however, because this refers to the "ideal human face" determined by scientists and artists.
For example, the total width of the two front teeth in the upper jaw over their height gives a golden ratio. The width of the first tooth from the centre to the second tooth also yields a golden ratio. These are the ideal proportions that a dentist may consider. Some other golden ratios in the human face are:
Length of face / width of face,
Distance between the lips and where the eyebrows meet / length of nose,
Length of face / distance between tip of jaw and where the eyebrows meet,
Length of mouth / width of nose,
Width of nose / distance between nostrils,
Distance between pupils / distance between eyebrows.
Golden Proportion in the Lungs
In a study carried out between 1985 and 1987 (5), the American physicist B. J. West and Dr. A. L. Goldberger revealed the existence of the golden ratio in the structure of the lung. One feature of the network of the bronchi that constitutes the lung is that it is asymmetric. For example, the windpipe divides into two main bronchi, one long (the left) and the other short (the right). This asymmetrical division continues into the subsequent subdivisions of the bronchi. (6) It was determined that in all these divisions the proportion of the short bronchus to the long was always 1/1.618.
THE GOLDEN RECTANGLE AND THE DESIGN IN THE SPIRAL
A rectangle the proportion of whose sides is equal to the golden ratio is known as a "golden rectangle." A rectangle whose sides are 1.618 and 1 units long is a golden rectangle. Let us assume a square drawn along the length of the short side of this rectangle and draw a quarter circle between two corners of the square. Then, let us draw a square and a quarter circle on the remaining side and do this for all the remaining rectangles in the main rectangle. When you do this you will end up with a spiral.
The British aesthetician William Charlton explains the way that people find the spiral pleasing and have been using it for thousands of years stating that we find spirals pleasing because we are easily able to visually follow them. (7)
The spirals based on the golden ratio contain the most incomparable designs you can find in nature. The first examples we can give of this are the spiral sequences on the sunflower and the pine cone. In addition to this, an example of Almighty Allah's flawless creation and how He has created everything with a measure, the growth process of many living things also takes place in a logarithmic spiral form. The curves in the spiral are always the same and the main form never changes no matter their size. No other shape in mathematics possesses this property. (8)
The Design in Sea Shells
 The flawless design in the nautilus shell contains the golden ratio. |
When investigating the shells of the living things classified as mollusks, which live at the bottom of the sea, the form and the structure of the internal and external surfaces of the shells attracted the scientists' attention:
The internal surface is smooth, the outside one is fluted. The mollusk body is inside shell and the internal surface of shells should be smooth. The outside edges of the shell augment a rigidity of shells and, thus, increase its strength. The shell forms astonish by their perfection and profitability of means spent on its creation. The spiral's idea in shells is expressed in the perfect geometrical form, in surprising beautiful, "sharpened" design. (9)
The shells of most mollusks grow in a logarithmic spiral manner. There can be no doubt, of course, that these animals are unaware of even the simplest mathematical calculation, let alone logarithmic spirals. So how is it that the creatures in question can know that this is the best way for them to grow? How do these animals, that some scientists describe as "primitive," know that this is the ideal form for them? It is impossible for growth of this kind to take place in the absence of a consciousness or intellect. That consciousness exists neither in mollusks nor, despite what some scientists would claim, in nature itself. It is totally irrational to seek to account for such a thing in terms of chance. This design can only be the product of a superior intellect and knowledge, and belongs to Almighty Allah, the Creator of all things:
"My Lord encompasses all things in His knowledge so will you not pay heed?" (Surat al-An'am, 80)
Growth of this kind was described as "gnomic growth" by the biologist Sir D'Arcy Thompson, an expert on the subject, who stated that it was impossible to imagine a simpler system, during the growth of a seashell, than which was based on widening and extension in line with identical and unchanging proportions. As he pointed out, the shell constantly grows, but its shape remains the same. (10)
One can see one of the best examples of this type of growth in a nautilus, just a few centimetres in diameter. C. Morrison describes this growth process, which is exceptionally difficult to plan even with human intelligence, stating that along the nautilus shell, an internal spiral extends consisting of a number of chambers with mother-of-pearl lined walls. As the animal grows, it builds another chamber at the spiral shell mouth larger than the one before it, and moves forward into this larger area by closing the door behind it with a layer of mother-of-pearl. (11)
The scientific names of some other marine creatures with logarithmic spirals containing the different growth ratios in their shells are:
Haliotis Parvus, Dolium Perdix, Murex, Fusus Antiquus, Scalari Pretiosa, Solarium Trochleare.
Ammonites, extinct sea animals that are today found only in fossil form, too, had shells developing in logarithmic spiral form.
Growth in a spiral form in the animal world is not restricted to the shells of mollusks. Animals such as antelopes, goats and rams complete their horn development in spiral forms based on the golden ratio. (12)
The Golden Ratio in the Hearing and Balance Organ
The cochlea in the human inner ear serves to transmit sound vibrations. This bony structure, filled with fluid, has a logarithmic spiral shape with a fixed angle of ?=73°43´ containing the golden ratio.
Horns and Teeth That Grow in a Spiral Form
Examples of curves based on the logarithmic spiral can be seen in the tusks of elephants and the now-extinct mammoth, lions' claws and parrots' beaks. The eperia spider always weaves its webs in a logarithmic spiral. Among the micro-organisms known as plankton, the bodies of globigerinae, planorbis, vortex, terebra, turitellae and trochida are all constructed on spirals.
THE GOLDEN RATIO IN THE MICRO WORLD
Geometrical shapes are by no means limited to triangles, squares, pentagons or hexagons. These shapes can also come together in various ways and produce new three-dimensional geometrical shapes. The cube and the pyramid are the first examples that can be cited. In addition to these, however, there are also such three-dimensional shapes as the tetrahedron (with regular four faces), octahedron, dodecahedron and icosahedron, that we may never encounter in our daily lives and whose names we may never even have heard of. The dodecahedron consists of 12 pentagonal faces, and the icosahedron of 20 triangles. Scientists have discovered that these shapes can all mathematically turn into one another, and that this transformation takes place with ratios linked to the golden ratio.
Three-dimensional forms that contain the golden ratio are very widespread in micro-organisms. Many viruses have an icosahedron shape. The best known of these is the Adeno virus. The protein sheath of the Adeno virus consists of 252 protein subunits, all regularly set out. The 12 subunits in the corners of the icosahedron are in the shape of pentagonal prisms. Rod-like structures protrude from these corners.
The first people to discover that viruses came in shapes containing the golden ratio were Aaron Klug and Donald Caspar from Birkbeck College in London in the 1950s. The first virus they established this in was the polio virus. The Rhino 14 virus has the same shape as the polio virus.
Why is it that viruses have shapes based on the golden ratio, shapes that it is hard for us even to visualise in our minds? A. Klug, who discovered these shapes, explains:
My colleague Donald Caspar and I showed that the design of these viruses could be explained in terms of a generalization of icosahedral symmetry that allows identical units to be related to each other in a quasi-equivalent way with a small measure of internal flexibility. We enumerated all the possible designs, which have similarities to the geodesic domes designed by the architect R. Buckminster Fuller. However, whereas Fuller's domes have to be assembled following a fairly elaborate code, the design of the virus shell allows it to build itself. (14)
Klug's description once again reveals a manifest truth. There is a sensitive planning and intelligent design even in viruses, regarded by scientists as "one of the simplest and smallest living things." (15) This design is a great deal more successful than and superior to those of Buckminster Fuller, one of the world's most eminent architects.
The dodecahedron and icosahedron also appear in the silica skeletons of radiolarians, single-celled marine organisms.
Structures based on these two geometric shapes, like the regular dodecahedron with feet-like structures protruding from each corner, and the various formations on their surfaces make up the varying beautiful bodies of the radiolarians. (16)
As an example of these organisms, less than a millimetre in size, we may cite the icosahedron based Circigonia Icosahedra and the Circorhegma Dodecahedra with dodecahedron skeleton. (17)
The Golden Ratio in DNA
The molecule in which all the physical features of living things are stored, too, has been created in a form based on the golden ratio. The DNA molecule, the very program of life, is based on the golden ratio. DNA consists of two intertwined perpendicular helixes. The length of the curve in each of these helixes is 34 angstroms and the width 21 angstroms. (1 angstrom is one hundred millionth of a centimetre.) 21 and 34 are two consecutive Fibonacci numbers.
The Golden Ratio in Snow Crystals
The golden ratio also manifests itself in crystal structures. Most of these are in structures too minute to be seen with the naked eye. Yet you can see the golden ratio in snow flakes. The various long and short variations and protrusions that comprise the snow flake all yield the golden ratio. (18)
THE GOLDEN RATIO IN SPACE
In the universe there are many spiral galaxies containing the golden ratio in their structures.
The Golden Ratio in Physics
You encounter Fibonacci series and the golden ratio in fields that fall under the sphere of physics. When a light is held over two contiguous layers of glass, one part of that light passes through, one part is absorbed, and the rest is reflected. What happens is a "multiple reflection." The number of paths taken by the ray inside the glass before it emerges again depends on the number of reflections it is subjected to. In conclusion, when we determine the number of rays that re-emerge, we find that they are compatible with the Fibonacci numbers.
The fact that a great many unconnected animate or inanimate structures in nature are shaped according to a specific mathematical formula is one of the clearest proofs that these have been specially designed. The golden ratio is an aesthetic rule well known and applied by artists. Works of art based on that ratio represent aesthetic perfection. Plants, galaxies, micro-organisms, crystals and living things designed according to this rule imitated by artists are all examples of Allah's superior artistry. Allah reveals in the Qur'an that He has created all things with a measure. Some of these verses read:
… Allah has appointed a measure for all things. (Surat at-Talaq, 3)
… Everything has its measure with Him. (Surat ar-Ra'd, 8)
1- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 155.
2- Guy Murchie, The Seven Mysteries of Life, First Mariner Boks, New York, pp. 58-59.
3- J. Cumming, Nucleus: Architecture and Building Construction, Longman, 1985.
4- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 87.
5- A. L. Goldberger, et al., "Bronchial Asymmetry and Fibonacci Scaling." Experientia, 41 : 1537, 1985.
6- E. R. Weibel, Morphometry of the Human Lung, Academic Press, 1963.
7- William Charlton, Aesthetics: An Introduction, Hutchinson University Library, London, 1970.
8- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 77.
9- "The 'Golden' spirals and 'pentagonal' symmetry in the alive Nature," online at: http://www.goldenmuseum.com/index_engl.html
10- D'Arcy Wentworth Thompson, On Growth and Form, C.U.P., Cambridge, 1961.
11- C. Morrison, Along The Track, Withcombe and Tombs, Melbourne.
12- "The 'Golden' spirals and 'pentagonal' symmetry in the alive Nature," online at: http://www.goldenmuseum.com/index_engl.html
13- J. H. Mogle, et al., "The Stucture and Function of Viruses," Edward Arnold, London, 1978.
14- A. Klug, "Molecules on Grand Scale," New Scientist, 1561:46, 1987.
15- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 82.
16- Mehmet Suat Bergil, Doðada/Bilimde/Sanatta, Altýn Oran (The Golden Ratio in Nature/Science/Art), Arkeoloji ve Sanat Yayinlari, 2nd Edition, 1993, p. 85.
17- For bodies of radiolarians, see H. Weyl, Synnetry, Princeton, 1952.
18- Emre Becer, "Biçimsel Uyumun Matematiksel Kuralý Olarak, Altýn Oran" (The Golden Ratio as a Mathematical Rule of Formal Harmony), Bilim ve Teknik Dergisi (Journal of Science and Technology), January 1991, p.16.
19- V.E. Hoggatt, Jr. and Bicknell-Johnson, Fibonacci Quartley, 17:118, 1979.
Phi: That Golden Number
by Mark Freitag
Most people are familiar with the number Pi, since it is one of the most ubiquitous irrational numbers known to man. But, there is another irrational number that has the same propensity for popping up and is not as well known as Pi. This wonderful number is Phi, and it has a tendency to turn up in a great number of places, a few of which will be discussed in this essay.
One way to find Phi is to consider the solutions to the equation
When solving this equation we find that the roots are
x = 
~ 1.618... or x=
~ -.618...
~ 1.618... or x=~ -.618...We consider the first root to be Phi. We can also express Phi by the following two series.
Phi =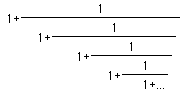 
or Phi = 
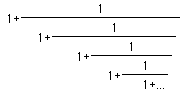or Phi = We can use a spreadsheet to see that these two series do approximate the value of Phi.
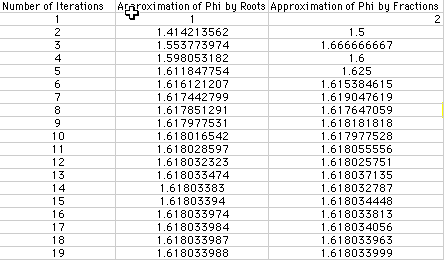
x =
. Squaring both sides we have
=
But this leads to the equation
which in turn leads to
and this has Phi as one of its roots. Similarly, it can be shown that the limit of the series with fractions is Phi as well. When finding the limit of the fractional series, we can take a side trip and see that Phi is the only number that when one is subtracted from it results in the reciprocal of the number.
Phi can also be found in many geometrical shapes, but instead of representing it as an irrational number, we can express it in the following way. Given a line segment, we can divide it into two segments A and B, in such a way that the length of the entire segment is to the length of the segment A as the length of segment A is to the length of segment B. If we calculate these ratios, we see that we get an approximation of the Golden Ratio.
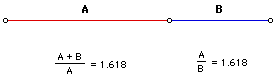
I have creted a GSP script for dividing a segment (given its endpoints) into the Golden ratio. If you would like to explore this, click here.
Another geometrical figure that is commonly associated with Phi is the Golden Rectangle. This particular rectangle has sides A and B that are in proportion to the Golden Ratio. It has been said that the Golden Rectangle is the most pleasing rectangle to the eye. If fact, it is said that any geometrical shape that has the Golden Ratio in it is the most pleasing to look at of those types of figures. Anyhow, here is a picture of the Golden Rectangle.
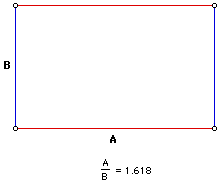
Keep this rectangle in mind, I'll be coming back to it later. But right now, I want to show where The Golden Ratio (Phi) pops up in other geometrical figures.
We can use the Golden Section to construct a regular pentagon.
If you would like to see a GSP script of this construction, click here. If we connect the vertices of the regular pentagon, we can get two different Golden Traingles. The blue triangle has its sides in the golden ratio with its base, and the red triangle has its base in the golden ratio with one of the sides.
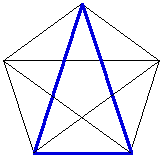
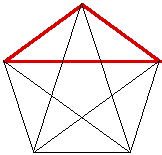
If we inscribe a regular decagon in a circle, the ratio of a side of the decagon to the radius of the circle forms the golden ratio.
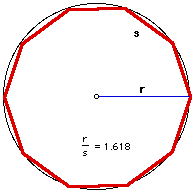
If we divide a circle into two arcs in the proportion of the Golden ratio, the central angle of the smaller arc marks off the Golden Angle, is 137.5 degrees.
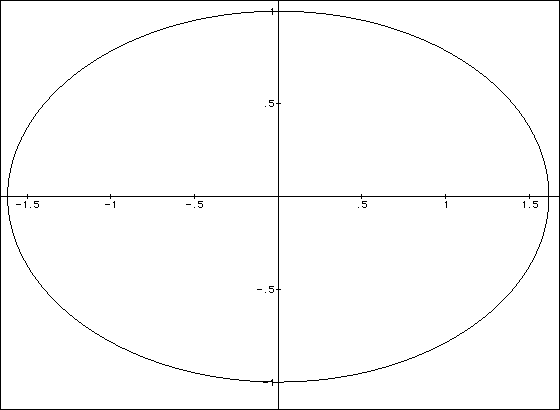
We can also form a Golden Ellipse. This ellipse has its two axes in the Golden Ratio.
Let's turn back to one of the Golden Triangles for a moment. If we take the isoceles triangle that has the two base angles of 72 degrees and we bisect one of the base angles, we should see that we get another Golden triangle that is similar to the first (Figure 1). If we continue in this fashion we should get a set of Whirling Triangles (Figure 2).
Figure 1 Figure 2
Out of these Whirling Triangles, we are able to draw a logarithmic spiral that will converge at the intersection of the the two blue lines in Figure 3.
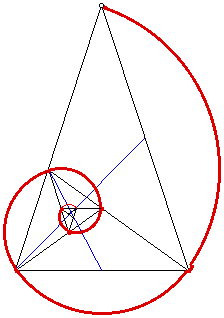
Figure 3
We can do a similar thing with the Golden Rectangle. We can make a set of Whirling Rectangles that produces a similar logarithmic spiral. Again this spiral converges at the intersection of the two blue lines, and these ratio of the lengths of these two lines is in the Golden Ratio.
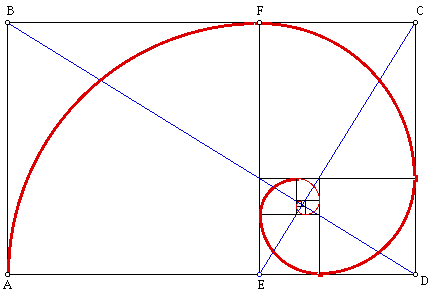
I will outline the proof that the ratio of the lengths of the two diagonals is indeed the Golden ratio. Assume that rectangle ABCD is a Golden Rectangle. Hence, AD/AB =AE/ED. But, FE = AE, and so FE/ED= Phi. Hence, rectangle FCDE is a Golden Rectangle. We have two similar rectangles and so since Phi = AD/EF then BD/CE = Phi.
An interesting thing happens when we work with these whirling rectangle. Suppose we take a rectangle of side 1 unit and a rectangle of side 2 units and we put them side to side in the following fashion and draw the appropriate segments to form a rectangle.
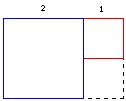
If we continue to create rectangles in this fashion we will get a series of whirling rectangles like the one of above. The following picture shows several such rectangles, and the lengths of their sides.
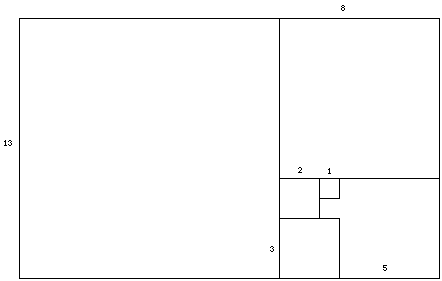
If we take ratios of the length we will see that the series of whirling rectangles will begin to estimate the Golden Ratio.
Hence as we increase the number of squares we get a figure that begins to look more and more like the Golden Rectangle. It might also be noticed that there is something special about the sides of the squares. If we list them we have, 1, 2, 3, 5, 8, 13, ... This of course is the famous Fibonacci sequence. As will be shown in the rest of the essay, the Fibonacci sequence and the golden ratio are intertwined with each other.
Leonardo Fibonacci began study of this sequence by posing the following problem in his book, Liber Abaci
How many pairs of rabbits will be produced in a year, beginning with a single pair , if in every month each pair bears a new pair which becomes productive from the second month on?
Of course, this problem gives rise to the sequence 1, 1, 2, 3, 5, 8, 13, ... in which any term after the first two can be found by summing the two previous terms. In functional notation we could write f(n) = f (n - 1) + f (n - 2) using f(0) = 1 and f(1) = 1.This particular sequence has some interesting properties. Instead of proving these, I will justify them by use of a spreadsheet.
I began by finding the first 40 Fibonacci numbers, which will be used in most of the demonstrations. The values can be found in column A. One of the first propeties that might be noticed is that for two positive integers a and b, if a | b then F(a) | F(b). For example, if a = 5 and
b = 10, then we have F(a) = 5 and F(b) = 55. The converse also holds true (If F(a) | F(b), then a | b), and proof of these two properties can be found in Maxfield and Maxfield (1972).
Another property of the Fibonnaci numbers is that no two consecutive numbers in the sequence have a common prime factor. As an example consider F(7) through F(10) (All though we can look at any of the first 40 numbers), and see that no consectutive pair has a common factor.
F(8) = 21 = 3 x 7
F(9) = 34 = 2 x 17
F(10 )= 55 =5 x 11
The proof is as follows.
Let F(n + 1) and F(n) be two consecutive Fibonnaci numbers and suppose that p | F(n + 1) and p | F(n) . Since F(n + 1)= F(n) + F(n - 1) , then p | F(n) + F(n - 1) and so p | F(n - 1). We also know that F(n) = F(n - 1) + F(n - 2), and by similar argument we get that p | F(n - 2). If we continue in this manner, we'll see that p divides every Fibonnaci number less than F(n + 1). Hence p | F(2) and p | F(3). Since F(2) = 2 and F(3) = 3, then p must equal 1. Therefore, 1 is the only number that will divide both F(n + 1) and F(n) and we conclude that they are relatively prime.
Another property that is verifiable by looking at the first forty terms of the sequence, is that the Fibonnaci sequence is complete with respect to the positive integers. This means that every positive integer can be written as the sum of finite terms from the sequence with no term being used more than once. For example, consider the positive integer 257.
This representation is not unique since
The proof of this property is a straight forward inductive proof and can be found in Maxfield and Maxfield (1972).
As was seen with the whirling rectangles, the ratio of consectutive Fibonacci numbers begins to apporximate the Golden Ratio. A spreadsheet can be used to see that this is more clearly the case. Values of these ratios can be found in column B.
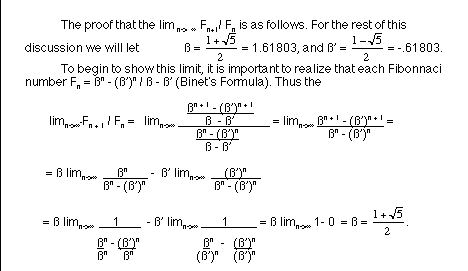
The second ratio that was considered was the ratio of every other term, or F(n + 2 )/ F(n). The values for the computed ratios for n = 1 to 40 are found in column C. As n increased, it could be seen that there was again a limiting value of approximately 2.61803. This number also has significance with regard to the golden ratio. We know that ß is one solution to the equation x^2 = x + 1, and this equation tells us that ß^2 = ß + 1. When we do the arithmetic, we find that ß^2 = 2.61803. The conclusion that we can then make from this is that the ratio of F(n + 2 )/ F(n) is an estimate of ß^2, and this estimate gets better as n gets larger.
Other ratios were of interest as well and the third ratio to be considered was the ratio of every third term, or F(n + 3 )/ F(n). The values for the computed ratios for n = 1 to 40 are found in column D. As n increased, it could be seen that there was again a limiting value of approximately 4.23607. This number also has significance with regard to the golden ratio. If we consider the system of equations
x^2 = x + 1
and make a substitution, we find that x^3 = 2x + 1. This means that if ß was a solution to the equation x^2 = x + 1, then we should be able to conclude that ß^3 = 2ß + 1. So going through the arithmetic, we find that 2ß + 1= 2.61803. So the next connection that we make is that the ratio of
F(n + 2) / F(n) has a limiting value of ß^3.
Finally the fourth ratio to be considered was the ratio of every fourth term, or F(n + 4) / F(n). The values for the computed ratios for n = 1 to 40 are found in column E of the spreadsheet. As n increased, it could be seen that there was a limiting value of approximately 6.8541, and again this number has connections with the golden ratio. If we consider the system of equations
x^3 = x^2 + x
x^2 = x + 1
and make appropriate substitutions, we find that x^4 = 3x + 2. This means that if ß was a solution to the equation x^2 = x + 1, then we should be able to conclude that ß^4 = 3ß + 2. So going through the arithmetic, we find that 3ß + 2 = 6.8541. So the final connection we make is that the ratio of
F(n + 4) / F(n) has a limiting value of ß^4.
So what hypotheses can we make from this sequence of discussions? First, if we were to continue to solve equations, we could find a general formula for any power of x. This being
Using this equation, we can compute any power of ß simply substituting ß in for x. The proofs of these facts should follow from a simple inductive process. The last hypothesis that we make is that, for any integer k> 1,
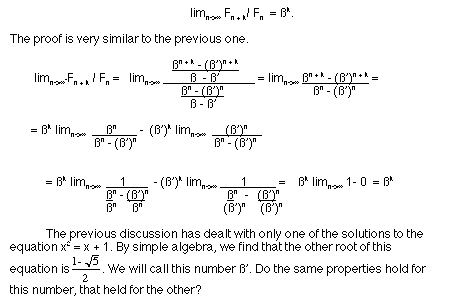
The first question to be answered would be, "Is ß' the limiting value of some ratio of the Fibonnaci numbers as they go towards infinity? The answer is yes. If we consider the following ratio
F(n)/ F(n + 1) and consider the limit of this as n goes to infinity, we do get the value of ß' = -.61803. The value of the first thirty-nine ratios can be found in column F of the spreadsheet. We can also go through a similar process with the ratios of F(n)/F(n + 2 ), F(n)/F(n + 3 ), and F(n)/F(n +4), and see that the same properties hold for ß' that held for ß. The values for these ratios are in the spreadsheet columns G, H, and I respectively.
The spreadsheet was used in another way to help analyze the Fibonnaci sequence. It allowed us to easily change the first two numbers of the sequence and therefore allowing us to change the entire sequence. Many different values were tried including positive and negative integers and decimals of varying length. The very interesting event that happened was that the ratios always estimated their appropriate power of ß of ß'.
Also, the spreadsheet enabled us to look at the formula F(n - 1) * F(n + 1) - F(n)^2 for n a positive integer less than or equal to 40. The resulting values are in the spreadsheet column J. The values are somewhat interesting. When n is even we get 1, and when n is odd we get -1. Hence, we hypothesize that
\
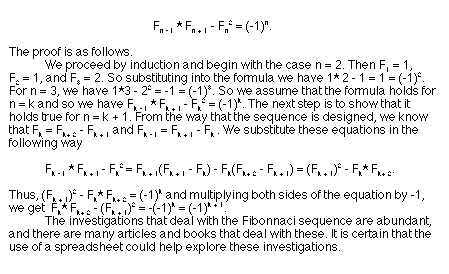